Principle of Mathematical Induction

Introduction:

       Mathematical induction is a mathematical proof technique. As a mathematical technique of proving things, mathematical induction is essentially used to prove the property of natural numbers.

The principle of mathematical induction:

Statement:

Let  be a given statement where  is nature number such that

(i)      The statement  is true for, i.e.,  is true.

(ii)   Let the statement is true for  then the statement is also true for, where  is some positive integer.

                 Then   is true for all natural numbers.

Example: For all, prove that.

Proof:

                        Let  be the given statement.

i.e.,.

For,

LHS

RHS

Hence LHS = RHS.

So,  is true.

 

Let  is true for some positive integer, i.e.

 

Now

        (Using (1))

    

    

 

Therefore the statement  is true for , when it is for .

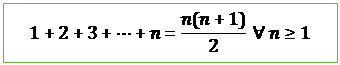Text Box: 1+2+3+⋯+n=(n(n+1))/2 ∀ n≥1Then by Principle of mathematical induction  is true for all natural number .

Hence.                                                                                      (Proof)

 

Exercise 4.1 NCERT Book

Prove the following using the principle of mathematical induction .

 1. 

            Proof:

                         Let  be the given statement.

                        i.e.,  .

                        For ,

                        LHS

                        RHS

                        Hence LHS = RHS.

                        So,  is true.

            Let  is true for some positive integer , i.e.

             

Now

        (Using (1))

    

    

   

  

            Therefore the statement  is true for , when it is true for .

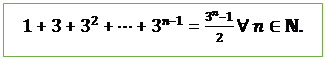Text Box: 1+3+3^2+⋯+3^(n-1)=(3^n-1)/2∀ n∈N.            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                    (Proof)

 

2.

            Proof:

                        Let  be the given statement.

                        i.e.,.

                        For ,

                        LHS

                        RHS

                        Hence LHS = RHS.

                        So,  is true.

            Let  is true for some positive integer , i.e.

             

            Now

        (Using (1))

    

    

    

    

   

  

  

            Therefore the statement  is true for , when it is true for .

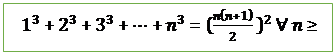Text Box: 〖 1〗^3+2^3+3^3+⋯+n^3=(n(n+1)/2 )^2∀ n≥1.            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                    (Proof)

 

3. 

            Proof:

             Let  be the given statement.

            i.e. 

            For   ,

            LHS

            RHS

            Hence LHS = RHS.

            So,  is true.

            Let  is true for some positive integer , i.e.

 

Now

       (Using (1))

    

    

    

    

   

  

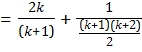
            Therefore the statement  is true for , when it is true for .

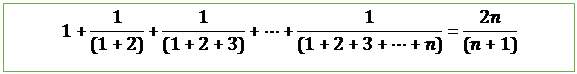Text Box: 1+1/((1+2))+1/((1+2+3))+⋯+1/((1+2+3+⋯+n))=2n/((n+1))            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                                                                                           (Proof).

 

 

4.   

Proof:

         Let  be the given statement.

        i.e.

        For ,

        LHS

        RHS

        Hence LHS = RHS.

        So,  is true.

Let  is true for some positive integer, i.e.

       

Now

        (Using (1))

    

    

    

            Therefore the statement  is true for , when it is true for .

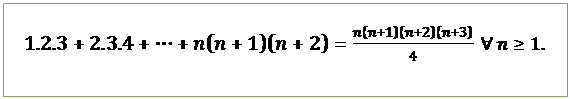Text Box: 1.2.3+2.3.4+⋯+n(n+1)(n+2)=n(n+1)(n+2)(n+3)/4 ∀ n≥1.            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                                                                                    (Proof).

 

 

 

5. 

            Proof:

            Let  be the given statement.

            i.e. 

            For ,

            LHS

            RHS

            Hence LHS = RHS.

            So,  is true.

            Let  is true for some positive integer , i.e.,

                         

            Now

        (using (1))

    

    

    

    

   

Therefore the statement  is true for , when it is true for .

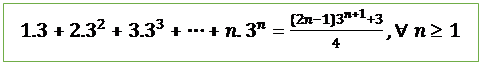Text Box: 1.3+〖2.3〗^2+〖3.3〗^3+⋯+n.3^n=((2n-1)3^(n+1)+3)/4,∀ n≥1 Then by Principle of mathematical induction  is true for all natural number .

Hence                                                                                                                           (Proof)

 

 

6.  

Proof:

      Let  be the given statement.

i.e.

For ,

LHS

RHS

Hence LHS = RHS.

So,  is true.

Let  is true for some positive integer , i.e.

 

Now

        (Using (1))

    

    

    

     Therefore the statement  is true for , when it is true for .

Text Box: 1.2+2.3+3.4+⋯+n(n+1)=[n(n+1)(n+2)/3],∀ n≥1     Then by Principle of mathematical induction  is true for all natural number .

      Hence                                                                                                                                       (      Proof

 

 

7. 

         Proof:

            Let  be the given statement.

i.e.

For ,

LHS

RHS

Hence LHS = RHS.

So,  is true.

Let  is true for some positive integer , i.e.

 

Now

       (using (1))

      

      

    

    

   

  

            Therefore the statement  is true for , when it is true for .

            Then by Principle of mathematical induction  is true for all natural number .

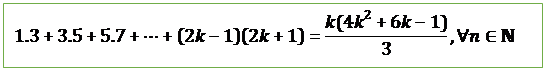Text Box: 1.3+3.5+5.7+⋯+(2k-1)(2k+1)=(k(4k^2+6k-1))/3,∀n∈N            Hence                                                                                                                                           (Proof).

 

 

8. 

         Proof:

                        Let  be the given statement.

                        i.e.

                        For,

                        LHS

                        RHS

                        Hence LHS = RHS.

                        So,  is true.

            Let  is true for some positive integer , i.e.

 

            Now

       (Using (1))

    

    

    

            Therefore the statement  is true for , when it is true for .

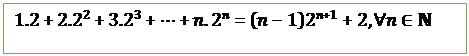Text Box: 1.2+〖2.2〗^2+〖3.2〗^3+⋯+n.2^n=(n-1) 2^(n+1)+2,∀n∈N            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                                                        (Proof).

 

9. 

      Proof:

                        Let  be the given statement.

                        i.e. 

                        For ,

                        LHS

                        RHS

            Hence LHS = RHS.

            So,  is true.

            Let  is true for some positive integer , i.e.

 

            Now

       (Using (1))

         

    

             Therefore the statement  is true for , when it is true for .

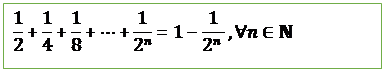Text Box: 1/2+1/4+1/8+⋯+1/2^n =1-1/(2^n ),∀n∈N            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                                (Proof).

 

 

10. 

        Proof:

                        Let  be the given statement.

                        i.e. 

                        For ,

                        LHS

                        RHS

                        Hence LHS = RHS.

                        So,  is true.

            Let  is true for some positive integer , i.e.

 

            Now

       (Using (1))

         

         

    

    

   

   

            Therefore the statement  is true for , when it is true for .

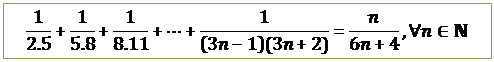Text Box: 1/2.5+1/5.8+1/8.11+⋯+1/((3n-1)(3n+2))=n/(6n+4),∀n∈N            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                                                                            (Proof).

 

11. 

           Proof:

             Let  be the given statement.

i.e.

For ,

LHS

RHS

Hence LHS = RHS.

So,  is true.

Let  is true for some positive integer , i.e.

  

Now

       (Using (1))

         

         

    

             Therefore the statement  is true for, when it is true for.

Text Box: a+ar+ar^2+⋯ar^(n-1)=(a(r^n-1))/(r-1),∀n∈N            Then by Principle of mathematical induction  is true for all natural number.

            Hence                                                                                                (Proof).

 

 

12.   is a multiple of.

        Proof:

            Let  be the given statement.

            i.e.,   is a multiple of .

            For ,

                         , which is multiple of

            So,  is true.    

            Let  is true for some positive integer , i.e.

                          is a multiple of

            Let

       

            Now

      (Using (1))

     , which is multiple of .   

            Therefore the statement  is true for , when it is true for .

Text Box: 3,∀n∈NText Box: n(n+1)(n+3)            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                      is a multiple of                             (Proof).

 

13.   is multiple of  .

         Proof:

            Let  be the given statement.

            i.e.,   is multiple of

            For ,

                          which is multiple of

            So,  is true.

            Let  is true for some positive integer , i.e.,

                          is multiple of

                         , where

            Now

       

    

     (Using (1))

    , which is divisible by.

            Therefore the statement  is true for, when it is true for.

Text Box: 27,∀ n≥1Text Box: 〖41〗^n-〖14〗^n            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                is multiple of                          .      (Proof).

 

14. 

        Proof:

            Let  be the given statement.

            i.e., 

            For ,

            LHS

            RHS

            Since

            So,  is true.

            Let  is true for some positive integer , i.e.,

                         

            Now

     

      (Using (1))

    

   

    

    

            Therefore the statement  is true for , when it is true for .

Text Box: (2n+7)<(n+3)^2,∀ n≥1            Then by Principle of mathematical induction  is true for all natural number .

            Hence                                                                (Proof).