Sequence and Series

Definition:

Sequence is nothing but the collection of well defined objects. In other words, this is a function from set of natural number to any set.

Sequence can be written as , or simply

Example

, are the examples of sequences.

Two types of sequences are there. One is finite sequence and other is infinite sequence.

Finite sequence a sequence is said to be finite sequence if it contain finite number of terms.

Example:

, , are the examples of finite sequence.

Infinite sequence a sequence is called infinite sequence if it is not finite sequence or it contain infinite number of terms.

Example:

, are examples of infinite sequence.

Note Any infinite sequence is usually denoted by it’s term or .

Let be a sequence. Here

and so on.

The above sequence can be written as, where is natural number. Similarly the sequence of odd natural number is written as.

Fibonacci sequence Let us consider a sequence.

Here, , , ,. . .. This sequence is called Fibonacci sequence.

Write the first 4 terms of each of the following sequences

1. , 2.

3. 4.

1. Here

Solution:

,

,

,

.

2. Here. To get the first 4 terms we have to put in .

Solution:

.

3. Given ………(1)

Solution:

Putting in (1) we have

.

4. Here . Hence we get

Solution:

.

Find the 20^th term of the sequence and 15^th term of the sequence

Solution:

20^th term of the sequence is given by

And 15^th term of the sequence is given by

.

Write the first five term of the sequence , and for all .

Solution:

Here given

Arithmetic progression (A.P.) A sequence is said to be arithmetic sequence or arithmetic progression if , where is called first term and the constant is called the common difference of the A.P.

If be the 1^st term and be the common difference of an A.P. then the standard form of the A.P. is

Note:

1. If a constant is added to each term of A.P. or subtracted from each term of A.P., then the resulting sequence will also be an A.P.

2. If each term of A.P is multiplied by a constant, then the resulting sequence will also be an A.P.

3. If each term of an A.P is divided by an non-zero constant, then each resultant sequence will again become an A.P.

General notation of arithmetic progression

: The 1^st term

: The last term

: The common difference

: The number of terms

: Sum of terms of A.P.

The last term and sum of term of an A.P., whose 1^st term and common difference is given by

And

Arithmetic mean Let and be two numbers. Then a number is said to be arithmetic mean of and if an A.P. is and is given by

Example: The arithmetic mean of and is .

Find the sum of odd integers from to .

Solution:

Here sequence is .

Hence, and

and.

In an A.P. the 1^st term is and the sum of 1^st five term is one-fourth of next five term. Show that 20^th term is .

Solution:

Here. Let be the common difference. Then 6^th term is .

Hence by the given condition we have

(Cancelling from both side)

20^th term is

.

In an A.P., if term is and term is . Prove that the sum of 1^st term is , where

Proof:

Let be the 1^st term and be the common difference of the A.P.

Then by given condition,

……… (1)

And ………. (2)

Subtracting (1) from (2) we have,

Putting the value of in (1)

Hence the sum of 1^st term is given by

(Proved).

If the sum of certain number of term of the A.P. is. Find the last term.

Solution:

Here,. Let the number of term is.

Or, .

Since number of terms cannot be fraction so.

So the number of term is.

Hence the last term is.

Insert terms in between and such that resulting sequence is in A.P.

Solution:

Let be term such that are in A.P.

Here , , .

Therefore

, ,

, ,

, .

If is the A.M. between and , then find the value of .

Solution:

By the given condition

Now,

.

Find the sum of terms of the A.P., whose term is.

Solution:

Let be the 1^st term and be the common difference of the A.P. then by given condition,

(1)

Putting in (1) we have,

So 1^st term is and

sum of terms

.

If the sum of term of an A.P. is , where and are constants. Find the common difference.

Solution:

Let be the given A.P. Then by the given condition

(1)

Putting in (1) we have,

,

.

Hence common difference .

The sum of terms of two arithmetic progression are in the ratio . Find the ratio of their 18^th terms.

Solution:

Let be the 1^st terms and be the common ratios respectively of the 1^st and 2^nd arithmetic progression. Then using the given condition,

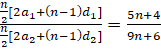
(1)

Now the ratio 18^th terms of 1^st and 2^nd A.P. is given by

(Putting in (1))

Geometric progression (G.P) A sequence is called geometric progression or G.P. if all terms are non-zero and , for , where is constant and is called common ratio.

Let be the 1^st term and be the common ratio of a G.P. Then G.P. is of the for

Example:

is G.P., since here and common ratio. Similarly is also a G.P. with common ratio.

Sum of terms of a G.P. Let the 1^st term of a G.P. be and common ratio be . Let be the sum of term of the G.P. that is

(1)

Then three cases may arise:

Case 1: If, then

Case 2: If, then multiplying both side of (1) by

(2)

Subtracting (2) by (1) we have,

Case 3: If, then similarly we get,

Geometric mean the geometric mean of the positive numbers and is.

Example: The geometric mean of and is.

Relation between A.M. and G.M. Let and be the arithmetic mean and geometric mean of the numbers and respectively. Then

And.

Now

.

Find the 8^th and 12^th terms of the G.P.

Solution:

Here and.

Therefore.

And.

The 5^th, 8th and 11^th term of a G.P. are and repectively. Show that.

Solution:

Let be the 1^st term and be the common ration of the G.P. Then

(1)

(2)

And (3)

Dividing (2) by (1) we have,

(4)

Again dividing (3) by (2) we have,

(5)

From (4) and (5) we get

.

Which term of the following sequences:

1. is

2. is

1. In this sequence, Let term of this sequence is.

Solution:

.

2. Let term of the sequence. And term of this sequence is.

Solution:

Here and

Hence

.

For what value of, the numbers are in G.P.?

Solution:

The numbers will be in G.P if

.

If and are A.M. and G.M. of two positive numbers then find the numbers.

Solution:

Let and be two numbers. Then

i.e., (1)

And

i.e., (2)

Now

(Using (1) and (2))

Taking positive sign, (3)

Adding (1) and (4),

Putting in (1), .

Now taking negative sign (4)

Adding (1) and (4),

Putting in (1),

Thus the numbers are or respectively.

Find the value of so that may be the G.M. of the numbers and .

Solution:

From the given condition,

.

Insert three numbers between and so that the resulting sequence is a G.P.

Solution:

Let are three numbers between and.

Since forms a G.P., then

Taking,

, ,

And taking,

,
Therefore we can insert or in between and so that the resulting sequences are in G.P.