Dynamics of Uniform Circular Motion

Acceleration of a body moving in a circle of radius R with uniform speed  is  directed towards the centre. According to the second law of motion, the force  providing this acceleration is :

  =                               ------ (1)

where m is the mass of the body. This force directed forwards the centre is called the centripetal force.

For a stone rotated in a circle by a string, the centripetal force is provided by the tension in the string. The centripetal force for motion of a planet around the sun is the gravitational force on the planet due to the sun. For a car taking a circular turn on a horizontal road, the centripetal force is the force of friction.

The circular motion of a car on a flat road compared to the same on a banked road give an interesting application of the laws of motion.

Motion of a Car on a Level Road:

lmsm16.PNG

Circular motion of a car on a level road

Three forces act on the car. (above figure)

        i.            The weight of the car, mg

     ii.            Normal reaction, N

   iii.            Frictional force, f

As there is no acceleration in the vertical direction

   N – mg  =  0

 N  =  mg                              ------ (2)

The centripetal force required for circular motion is along the surface of the road, and is provided by the component of the contact force between road and the car tyres along the surface. This by definition is the frictional force. Note that it is the static friction that provides the centripetal acceleration. Static friction opposes the impending motion of the car moving away from the circle. Using equation (fs ≤ μs N) & (1) we get the result 

  f ≤ μs N  =  

          ≤   =  μsRg     [∵ N  =  mg]

which is independent of the mass of the car. This shows that for a given value of μs and R, there is a maximum speed of circular motion of the car possible, namely

         =                         ------ (3)

Motion of a Car on a Banked Road:

lmsm17.PNG

Circular motion of a car on a banked road

We can reduce the contribution of friction to the circular motion of the car if the road is banked (above figure). Since there is no acceleration along the vertical direction, the net force along this direction must be zero. Hence,

  N cos θ  =  mg + f sin θ             ------ (4a)

The centripetal force is provided by the horizontal components of N and f.

         N sin θ + f cos θ  =                          ------ (5a)

But f ≤ μsN

Thus to obtain  we put

   f  =  μsN

Substituting value of f in equ. (4a) & (5a), we get

  N cos θ  =  mg + μsN sin θ        ------ (4b)

    N sin θ + μsN cos θ  =                              ------ (5b)

We obtain

 N  = 

Substituting value of N in Eq. (5b), we get

      =   

or    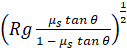                         =       ------ (6)

Comparing this with Eq. (3) that maximum possible speed of a car on a banked road is greater than that on a flat road.

For μs    0 in Eq. (6),

              =               ------ (7)

At this speed, frictional force is not needed at all to provide the necessary centripetal force. Driving at this speed on a banked road will cause little wear and tear of the tyres. The same equation also tells you that for  < , frictional force will be up the slope and that a car can be parked only if tan θ ≤ μs.

Problems:

1. A cyclist moves in a circular track of radius 100 m. If the coefficient of friction is 0.2, then what is the maximum speed with which the cyclist can take a turn without leaning inwards?

Solution:

To take a turn centripetal acceleration will be provided by the frictional force

∴                                                    =  μN

∴                                                       =  rμg        ------ (1)

Here radius of circular track,   r  = 100 m

Coefficient of friction,                μ  =  0.2

Gravitational acceleration,       g  =  9.8 m s−2

Substituting above values in eq (1) we get

          =  100 × 0.2 × 9.8

   =  196

∴                                                        =  14 m s−1

 

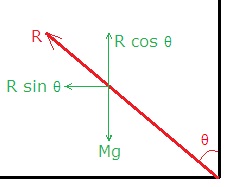
2. A motor-cyclist moving with a velocity of 72 km/hr on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20 meter. The acceleration due to gravity is 10 ms−2. In order to avoid sliding, he must not bend with respect to the vertical plane by an angle greater than..?

Solution:

s7.jpg

Velocity of moving motor-cyclist  =  72 km/hr

Radius of curvature of the road    =  20 m

Acceleration due to gravity             =  10 ms−2

R is the reaction the ground

  72 Km/hr  =  20 m/s

From figure it is clear that R cos θ  =  mg and R sin θ  = 

tan θ  = 

tan θ  =   

tan θ  =  2 

       θ  =  tan−1(2)

 

3. A train runs along an unbanked circular track of radius 30 m at a speed of 54 km/h. The mass of the train is 106 kg. What is the angle of banking required to prevent wearing out of the rail?

Solution:

Radius of the circular track,  r    30 m

Speed of the train,                      =  54 km/h

 =  15 m/s

Mass of the train,                     m  =  106 kg

The angle of banking θ, is related to the radius (r) and speed () by the relation:

tan θ  =  

=   

= 

       θ  =  tan−1 (0.75)

=  36.87°

 

4. A bend in a level road has a radius of 100 m. Find the maximum speed which a car turning this bend may have without skidding, if the coefficient of friction between the car tyres and the road is 0.8.

Solution:

Here          r  =  100 m, μ  =  0.8, g  =  9.8 m s−2

∴                 f  =  μmg 

= 

or          =  

=   

=  28 m s−1

 

5. A car of mass 1500 kg is moving with a speed of 12.5 m/s on a circular path of radius 20 m on a level road. What should be the frictional force between the car and the road so that the car does not slip? What should be the value of the coefficient of friction to attain this force?

Solution:

Mass of the car    =  1500 kg

Speed of the car  =  12.5 m/s

       Frictional force  =  Required centripetal force

or                                f  =  

    = 

    =  1.172 × 104 N

But                             f    μR 

    =  μ mg

∴ Coefficient of fricton,

           μ  =   

   =   

   =  0.8

 

6. A string breaks under a load of 4.8 kg. A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle. Calculate the greatest no of revolutions that the mass can make without breaking the string.

Solution:

Here      m  =  0.5 kg, r  =  2 m, g  =  9.8 m s−2

The maximum tension that the string can withstand,

       F  =  4.8 kg wt

=  4.8 × 9.8 N

Let the maximum number of revolutions per second  = 

Now          F  =  mrω2 

=  mr(2π)2 

=  4π2 mr

or              =   

=   

=  1.215

or                = 

=  1.102 rps

=  1.102 × 60

=  66.13 rpm

 

7. A particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, calculate the tension in the string. 

Solution:

Here  m  =  21 g, r  =  70 cm

Period of revolution, T  =  2s

∴   Tension  =  mrω2 

=  mr

=  21 × 70 ×

=  14520 dyne

 

8. A 100 g weight is tied to the end of a string is whirled around in a horizontal circle of radius 15 cm at the rate of 3 rev./sec. What is the tension in the string?

Solution:

Here        m  =  0.1 kg, r  =  0.15 m,   =  3 rps

       ω  =  2 

=  2π × 3

=  6 π rads−1

       T  =  mrω2 

=  0.3 × 0.15 × (6π)2

=  5.334 N