Mutual
Induction
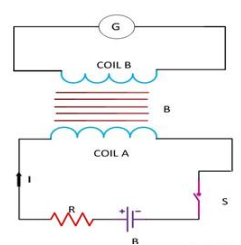
Whenever there is a
change in the magnetic flux linked with a coil, there is also a change of flux
linked with the neighbouring coil, producing an
induced emf in the second coil. This phenomenon of
producing an induced emf in a coil due to the change
in current in the other coil is known as mutual induction.
Ø Coil A
and B are two coils placed close to
each other as shown in figure. A is
connected to a battery B through a
switch S. B is connected to a galvanometer G.
Ø On pressing switch, current in A starts increasing from zero to a
maximum value. As the low of current increases, the magnetic flux linked with A increases.
Therefore, magnetic flux linked with B
also increases producing an induced emf in B.
Ø Now, the galvanometer shows the deflection.
According to Lenz’s law the induced current in B would oppose the increase in current in A by flowing in a direction opposite to the current in A, thus delaying the growth of current
to the maximum value.
Ø When the switch ‘S’ is released, current starts decreasing from maximum to zero
value, consequently magnetic flux linked with A decreases.
Ø Therefore magnetic flux linked with B also decreases and hence, an emf is induced in B.
Ø According to Lenz’s law, the induced current in B flows in such a direction so as to
oppose the decrease in current in A
thus prolonging the decay of current.
Coefficient of
mutual induction:
is the current in coil A and 
is the
magnetic flux linked with coil B due to the current in coil A.
∴ α or = M
where M is a
constant of proportionality and is called the coefficient of mutual induction
or mutual inductance between the two coils.
If
then, 
Thus, coefficient
of mutual induction of two coils is numerically equal to the magnetic flux
linked with one coil when unit current flows through the neighbouring
coil. If 
is the
induced emf in the coil (B) at any
instant of time, then from the laws of electromagnetic induction.
M = 
If 
, then M
= -
Thus, the
coefficient of mutual induction of two coils is numerically equal to the emf induced in one coil when the rate of change of current
through the other coil is unity. The unit of coefficient of mutual induction is
henry.
One henry is
defined as the coefficient of mutual induction between a pair of coils when a
change of current of one ampere per second in one coil produces an induced emf of one volt in the other coil. The coefficient of
mutual induction between a pair of coils depends on the following factors:
(i) Size and shape of
the coils, number of turns and permeability of material on which the coils are
wound.
(ii) Proximity of the coils.
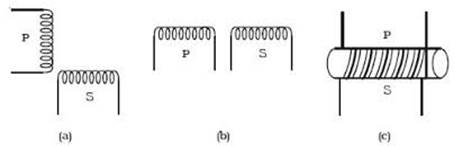
Two coils P and
S have
their axes perpendicular to each other as shown in figure. When a current is
passed through coil P, the magnetic
flux linked with S is small and
hence, the coefficient of mutual induction between the two coils is small.
The two coils are
placed in such a way that they have a common axis as shown in figure. When
current is passed through the coil P
the magnetic flux linked with coil S
is large and hence, the coefficient of mutual induction between the two coils
is large.
If the two coils are wound on a soft iron core the mutual
induction is very large.
Mutual Induction of Two Long
Solenoids
S1 and S2
are two long solenoids each of length l. The solenoid S2 is wound closely over the
solenoid S1 as shown in figure.
and 
are the
number of turns in the solenoids 
and 
respectively. Both the solenoids are considered
to have the same area of cross section A as they are closely wound together. 
is the current flowing through the solenoid . The magnetic field B1 produced at any point inside the solenoid due to the
current is
The magnetic flux linked with
each turn of is equal to 
.
Total magnetic flux linked with
solenoid having turns is
= 
A
Substituting
for 
where M is
the coefficient of mutual induction between
= 
= 
If the core is filled with a
magnetic material of permeability
= 
|
|
|
|
