Self Inductance

Self Inductance	Mutual inductance
Self-Induction is the characteristic of the coil itself.	Mutual induction is the characteristic of a pair of coils.
When the main current in the coil decreases, the induced current opposes the decay of current in the coil.	When the main current in the coil decreases, induced current developed in the neighbouring coil opposes the decay of current in the coil.
When the main current in the coil increases, the induced current opposes the growth of current in the coil.	When the main current in the coil increases, the induced current developed in the neighbouring coil opposes the growth of current in the coil.

The property of a coil which enables to produce an opposing induced emf in it when the current in the coil changes is called self induction.

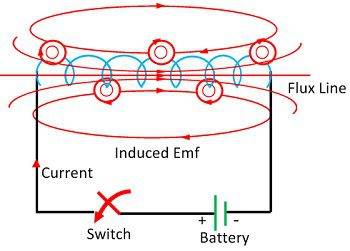
Ø A coil is connected in series with a battery and a switch as shown in figure. On pressing the switch, the current through the coil increases to a maximum value and correspondingly the magnetic flux linked with the coil also increases.

Ø An induced current flows through the coil which according to Lenz’s law opposes the further growth of current in the coil.

Ø On releasing the switch, the current through the coil decreases to a zero value and the magnetic flux linked with the coil also decreases.

Ø According to Lenz’s law, the induced current will oppose the decay of current in the coil.

Coefficient of self inductance:

When a current I flows through a coil, the magnetic flux (φ) linked with the coil is proportional to the current.

φ α I or φ = LI

where L is a constant of proportionality and is called coefficient of self induction or self inductance.

If I = 1A, φ = L × 1, then L = φ

Therefore, coefficient of self induction of a coil is numerically equal to the magnetic flux linked with a coil when unit current flows through it.

According to laws of electromagnetic induction

e = −

= − or e = − L

If 1A s^-1, then L = −e

The coefficient of self induction of a coil is numerically equal to the opposing emf induced in the coil when the rate of change of current through the coil is unity. The unit of self inductance is henry (H).

One henry is defined as the self-inductance of a coil in which a change in current of one ampere per second produces an opposing emf of one volt.

Self inductance of a long solenoid:

Let us consider a solenoid of N turns with length l and area of cross section A. It carries a current I. If B is the magnetic field at any point inside the solenoid, then

Magnetic flux per turn = B × area of each turn

But, B =

Magnetic flux per turn =

Hence, the total magnetic flux (φ) linked with the solenoid is given by the product of flux through each turn and the total number of turns.

φ =

φ = ------ (1)

If L is the coefficient of self induction of the solenoid, then

φ = LI ------ (2)

From equations (1) and (2)

LI =

L =

If the core is filled with a magnetic material of permeability μ,

then, L =

Energy associated with an inductor:

Whenever current flows through a coil, the self−inductance opposes the growth of the current. Hence, some work has to be done by external agencies in establishing the current. If e is the induced emf then,

e = − L

The small amount of work dw done in a time interval dt is

dw = e . I dt

= − L I. dt

The total work done when the current increases from 0 to maximum value () is

This work done is stored as magnetic potential energy in the coil.

∴ Energy stored in the coil

− = −

Negative sign is consequence of Lenz’s Law. Hence, quantitatively, the energy stored in an inductor is .